研究成果デモンストレーション

調波ベクトル分析（HVA）に基づく多チャネルブラインド音源分離

本ページは論文"Determined BSS based on time-frequency masking and its application to harmonic vector analysis"のデモンストレーションです．

ブラインド音源分離（BSS）とは，音源やマイクロフォンの位置等の混合系が未知の条件で，複数の音源が混合した観測信号のみから混合前の個々の音源信号を推定する技術です．音源の数とマイクロフォンの数が等しい場合は，決定的BSSと呼ばれます．BSSは，音声認識や補聴器，自動採譜等のあらゆる音アプリケーションのフロントエンド技術に用いることができます．

決定的BSSの歴史の中で最も成功を収めた手法は，2006年に提案された独立ベクトル分析（IVA）及び2016年に提案された独立低ランク行列分析（ILRMA）です（IVAとILRMAについてはコチラ）．これらの手法は音源モデルと呼ばれる，各音源の時間周波数構造に関する仮定を活用しています．IVAでは，各音源の時変な音量変化を表現するために周波数ベクトルモデルが仮定され，またILRMAでは，各音源で類似したスペクトルパターン（音色）が繰り返し生じることを表現するために低ランク時間周波数モデルが仮定されています．

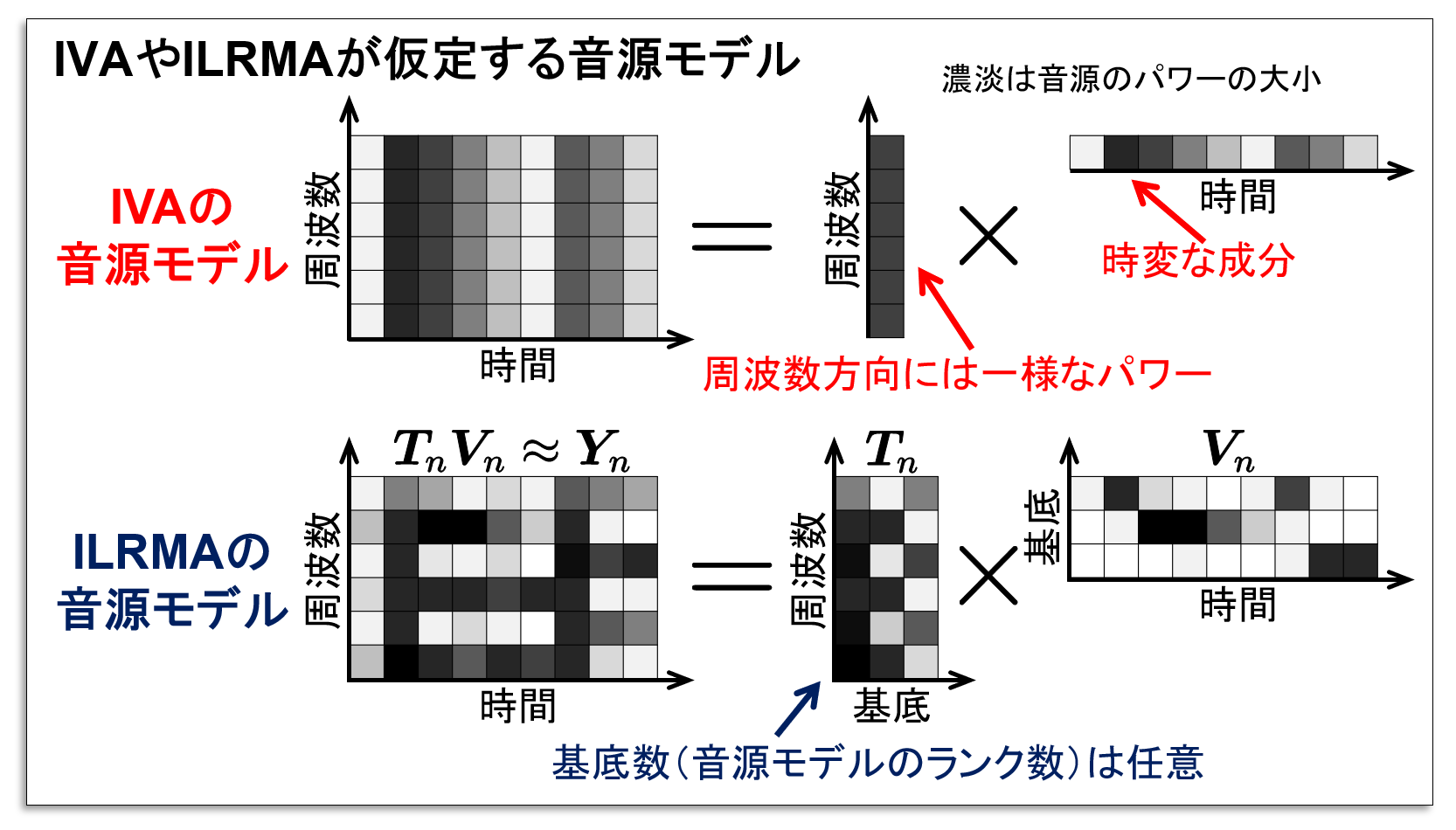
IVAとILRMAで仮定される音源モデルの図

正確な音源モデルはBSSの性能を向上させます．より効果的な音源モデルを探求するために，我々は時間周波数マスキングに基づく決定的BSS（TFMBSS）を提案しています．TFMBSSでは，いかなる時間周波数マスクもプラグアンドプレイで音源モデルに用いることができます．例えば，単一チャネル調波打撃音分離（HPSS）アルゴリズムを用いたTFMBSSも提案されています．

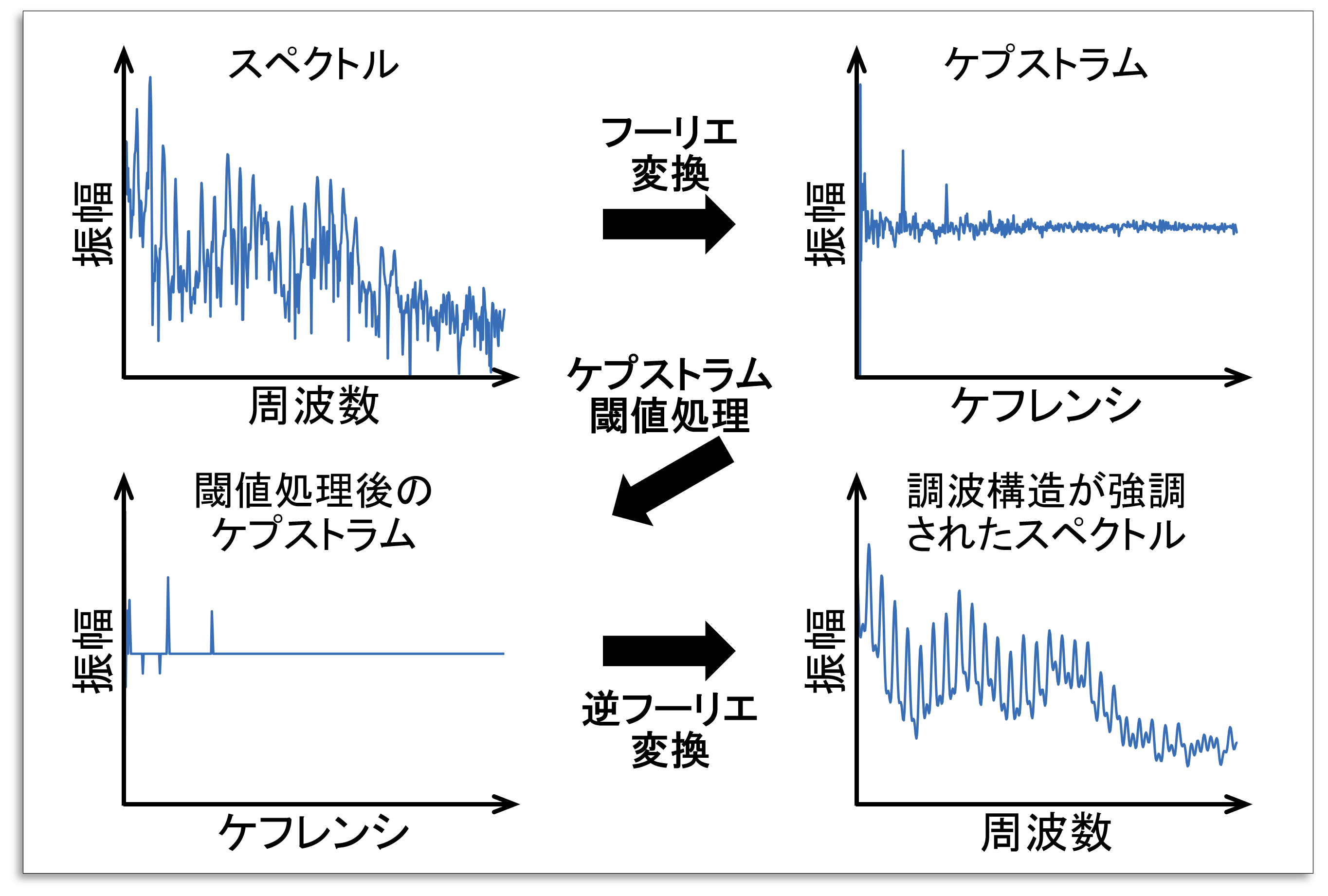
音声や音楽を含むほとんどすべての音源信号は調波構造を持ちます．調波構造とは，基本周波数とその倍音が生起する構造のことです．この基本原理に基づき，我々は調波ベクトル分析（HVA）を提案しています．HVAは，現在の各分離音源の調波構造をさらに強調するような時間周波数マスクを求めるTFMBSSです．図は典型的な音声のスペクトルと，その調波構造をケプストラム閾値処理により強調した例を示しています．左上図に示す音声の対数振幅スペクトルはフーリエ変換を施すことで，右上図のようにケプストラムに変換されます．このケプストラムを左下図のように閾値処理し，さらに逆フーリエ変換を施すことで，右下図のような調波構造が強調された対数振幅スペクトルを得ることができます．

ケプストラム閾値処理の図

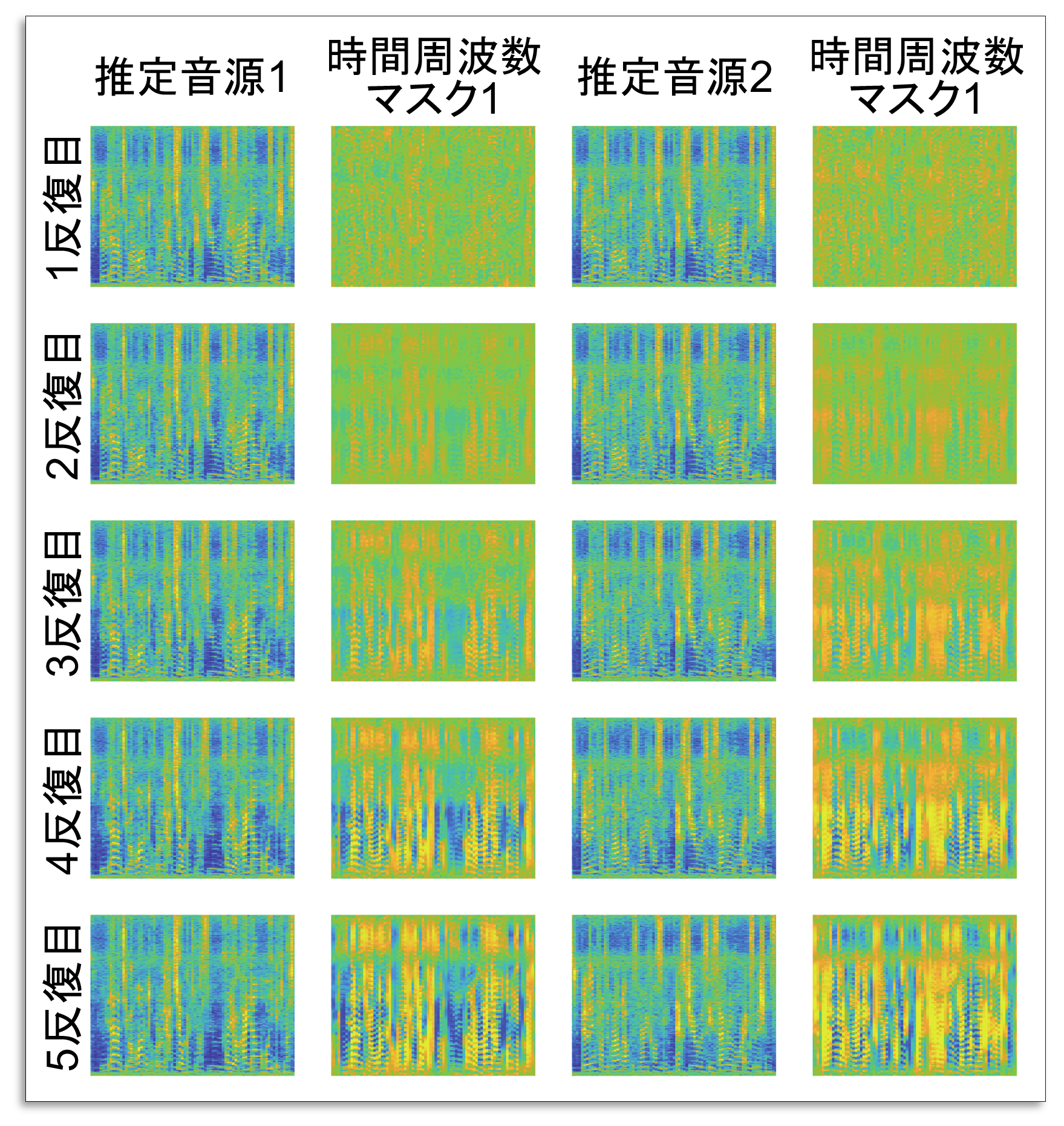
HVAの変数最適化では，前述の処理により，各推定音源の調波構造が反復的に強調されます．そのため，調波構造を持つ成分は自動的に同じ音源としてまとめられ，反復最適化の中で複数の音源が徐々に分離されていきます．この流れを図で示しています．

図は，2音源決定的BSSの条件下で，HVAの最初の5回の反復における（白色化された）時間周波数信号とマスクを示しています．各音源の時間周波数マスクが，調波構造（時間周波数領域ではストライプ状のパターン）を持つように劇的に変化していく様子を見ることができます．結果的に，推定音源は混合前の音源の時間周波数信号に近づいていきます．

反復毎の推定音源及びマスクの変化の図

下記のデモンストレーションでは，IVA，ILRMA，及びHVAの3手法で音声の混合信号をBSSしています．信号は2チャネルで観測した2音源の混合を用いており，残響時間130 msの部屋で実際に録音された混合信号です．

このデモに用いる音楽信号は全てSiSECから学術的研究を目的として拝借いたしました．

2チャネル2音源の実環境録音混合信号

入力信号 "dev1_female4_liverec_130ms_5cm_sim"

入力信号 (2人の女性話者混合)

IVAの分離信号

分離信号 1

分離信号 2

ILRMAの分離信号

分離信号 1

分離信号 2

HVAの分離信号

分離信号 1

分離信号 2

入力信号 "dev1_male4_liverec_130ms_5cm_sim"

入力信号 (2人の男性話者混合)

IVAの分離信号

分離信号 1

分離信号 2

ILRMAの分離信号

分離信号 1

分離信号 2

HVAの分離信号

分離信号 1

分離信号 2

ソースコード

Available online: K. Yatabe, "MATLAB code for harmonic vector analysis (HVA)," Jan. 2021, https://doi.org/10.24433/CO.9507820.v1.

参考文献

IVA
  • T. Kim, T. Eltoft, and T.-W. Lee, "Independent vector analysis: An extension of ICA to multivariate components," in Proc. Int. Conf. Independent Compon. Anal. Blind Source Separation, pp. 165–172, 2006.
  • A. Hiroe, "Solution of permutation problem in frequency domain ICA using multivariate probability density functions," in Proc. Int. Conf. Independent Compon. Anal. Blind Source Separation, pp. 601–608, 2006.
  • T. Kim, H. T. Attias, S.-Y. Lee, and T.-W. Lee, "Blind source separation exploiting higher-order frequency dependencies," IEEE Trans. Audio, Speech, Lang. Process., vol. 15, no. 1, pp. 70–79, 2007.
IVAにおける安定かつ高速な反復射影法（IP）に基づく最適化法
  • N. Ono, "Stable and fast update rules for independent vector analysis based on auxiliary function technique," in Proc. IEEE Workshop on App. of Signal Process. to Audio and Acoust., pp. 189–192, 2011.
ILRMA
  • D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Efficient multichannel nonnegative matrix factorization exploiting rank-1 spatial model," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., pp. 276–280, 2015.
  • D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Determined blind source separation unifying independent vector analysis and nonnegative matrix factorization," IEEE/ACM Trans. Audio, Speech, and Lang. Process., vol. 24, no. 9, pp. 1626–1641, 2016.
  • D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Determined blind source separation with independent low-rank matrix analysis," Audio Source Separation, S. Makino, Ed. (Springer, Cham, 2018), pp. 125–155.
TFMBSS
  • K. Yatabe and D. Kitamura, "Determined blind source separation via proximal splitting algorithm," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., pp. 776–780, 2018.
  • K. Yatabe and D. Kitamura, "Time-frequency-masking-based determined BSS with application to sparse IVA," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., pp. 715–719, 2019.
  • K. Yatabe and D. Kitamura, "Determined BSS based on time-frequency masking and its application to harmonic vector analysis," IEEE/ACM Trans. Audio, Speech, and Lang. Process., vol. 29, pp. 1609–1625, 2021.
HPSS-based TFMBSS
  • S. Oyabu, D. Kitamura, and K. Yatabe, "Linear multichannel blind source separation based on time-frequency mask obtained by harmonic/percussive sound separation," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., pp. 201–205, 2021.
HVA
  • K. Yatabe and D. Kitamura, "Determined BSS based on time-frequency masking and its application to harmonic vector analysis," IEEE/ACM Trans. Audio, Speech, and Lang. Process., vol. 29, pp. 1609–1625, 2021.