Demonstration of Research
Multichannel blind audio source separation based on independent low-rank matrix analysis (ILRMA)
Independent component analysis (ICA) is a statistical algorithm that separates independent audio sources without knowing recoding conditions such as room size, reverberation time, and locations of sources and microphones. This task is often called "blind source separation (BSS)" or "blind audio source separation (BASS)." In ICA, we assume statistical independence of audio sources, where the sources are assumed to be unrelated each other. ICA calculates a demixing system (matrix W in fig.) for the separation, where the demixing system corresponds to the inverse system of the mixture (matrix A in fig.).
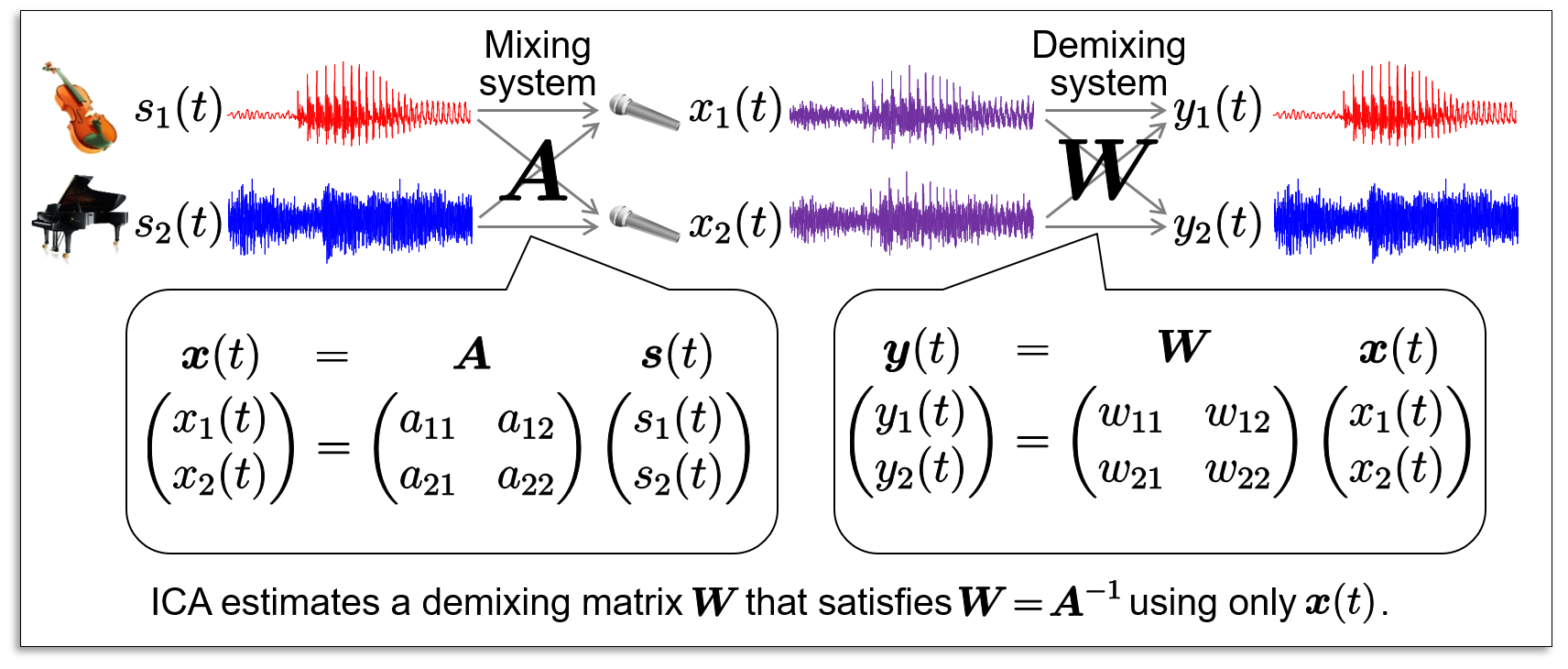
ICA can separate audio sources when the sources are mixed with no reverberation (instantaneous mixture). However, reverberation exists in a practical case, and the mixing system becomes a convolutive mixture. Since it is difficult to calculate deconvolution with only the observation, the observed signal is transformed into the time-frequency domain via a short-time Fourier transform (STFT), where the convolutive mixture is transformed into the instantaneous mixture, and ICA is applied. This BASS is called frequency-domain ICA (FDICA).
In FDICA, the observed signal is now a three-dimensional tensor that consists of time, frequency, and microphone (channel) axes. ICA is applied to each frequency, and frequency-wise demixing matrices are estimated to separate the sources. Since the signal components are complex-valued, a source distribution assumed in ICA for utilizing independent assumption becomes a complex distribution.
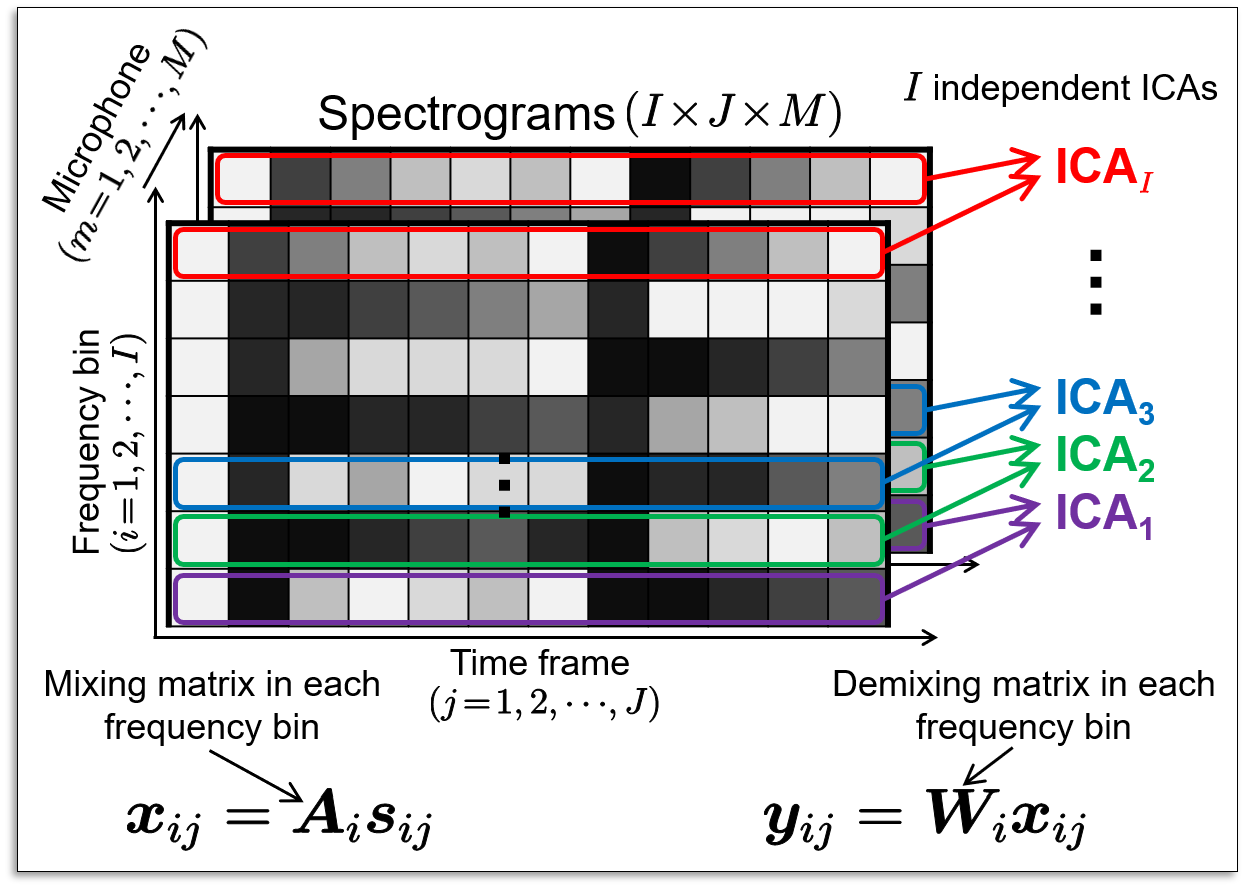
ICA cannot inherently determine an order of estimated (separated) sources. For example, when we apply ICA to a violin and piano mixture, first and second estimated sources could be either "violin and piano" or "piano and violin." This phenomenon causes a serious problem in FDICA.
Since FDICA employs independent ICAs in each frequency, the order of estimated sources becomes inconsistent (nonaligned) along the frequency axis. This problem is called "the permutation problem." Even if we apply inverse STFT to the nonaligned estimated sources, the sources are remixed. Thus, a permutation solver is required, which aligns the order of the estimated source for all frequency components.
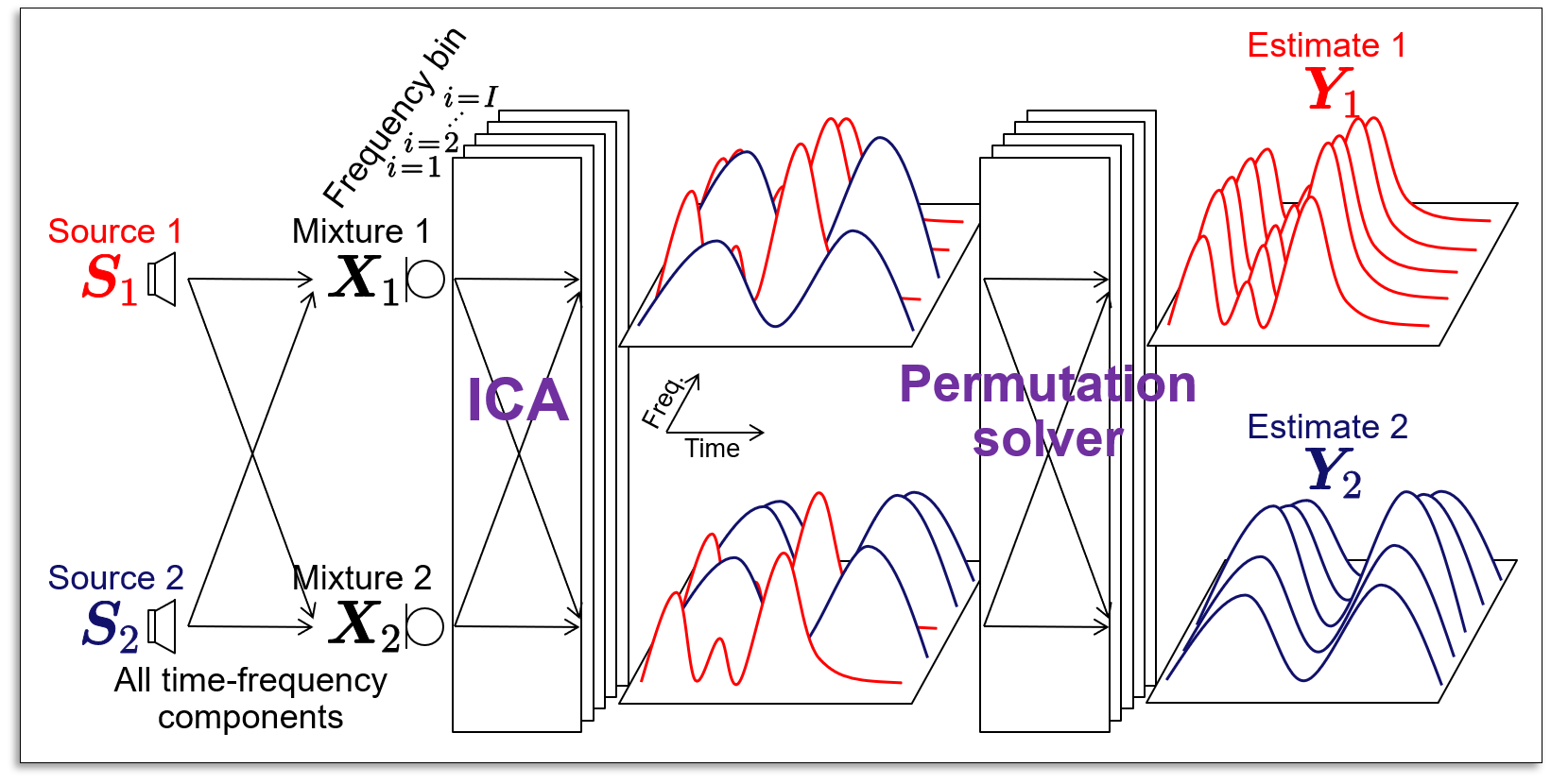
To solve the problem mentioned above, another assumption is required to FDICA to avoid encountering the permutation problem, namely, both the separated source components and the order of them should simultaneously be estimated. Independent vector analysis (IVA) is a popular method that assumes "co-occurrence of the frequency components of the same source" and avoids the permutation problem.
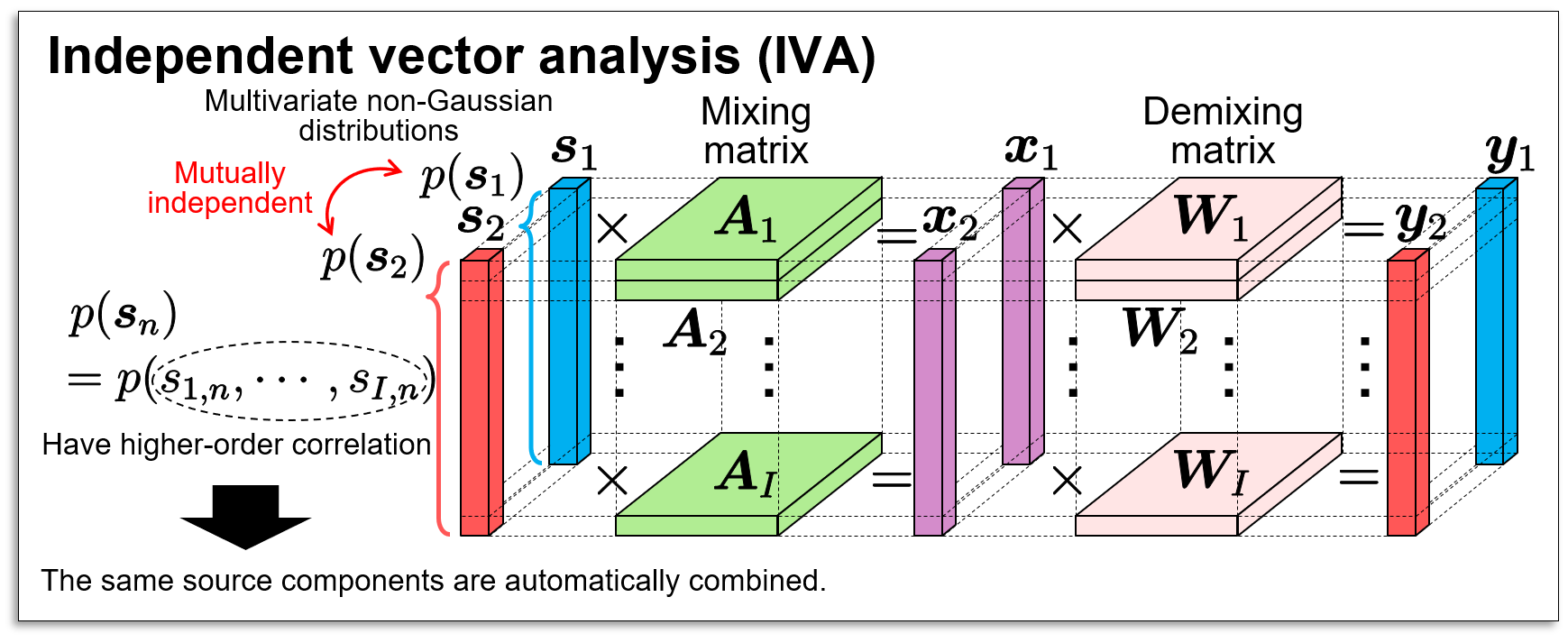
As a more detailed source assumption, we proposed to introduce the "co-occurrence of the time-frequency components of the same source" into FDICA, where time-frequency co-occurrence has a low-rank structure. This approach is called independent low-rank matrix analysis (ILRMA) and is a unification if FDICA and nonnegative matrix factorization (NMF). NMF models the time-frequency structure of the estimated source, and the frequency-wise demixing matrices are estimated without causing the permutation problem. Since the source model is more precise compared with that of IVA, the source separation accuracy tends to be better in many cases. In addition, iterative projection (IP) is introduced to ILRMA, where IP is a fast and convergence-guaranteed optimization algorithm for the demixing matrix in ICA and IVA. Thanks to IP-based parameter optimization, ILRMA achieves satisfactory computational efficiency in a practical situation.
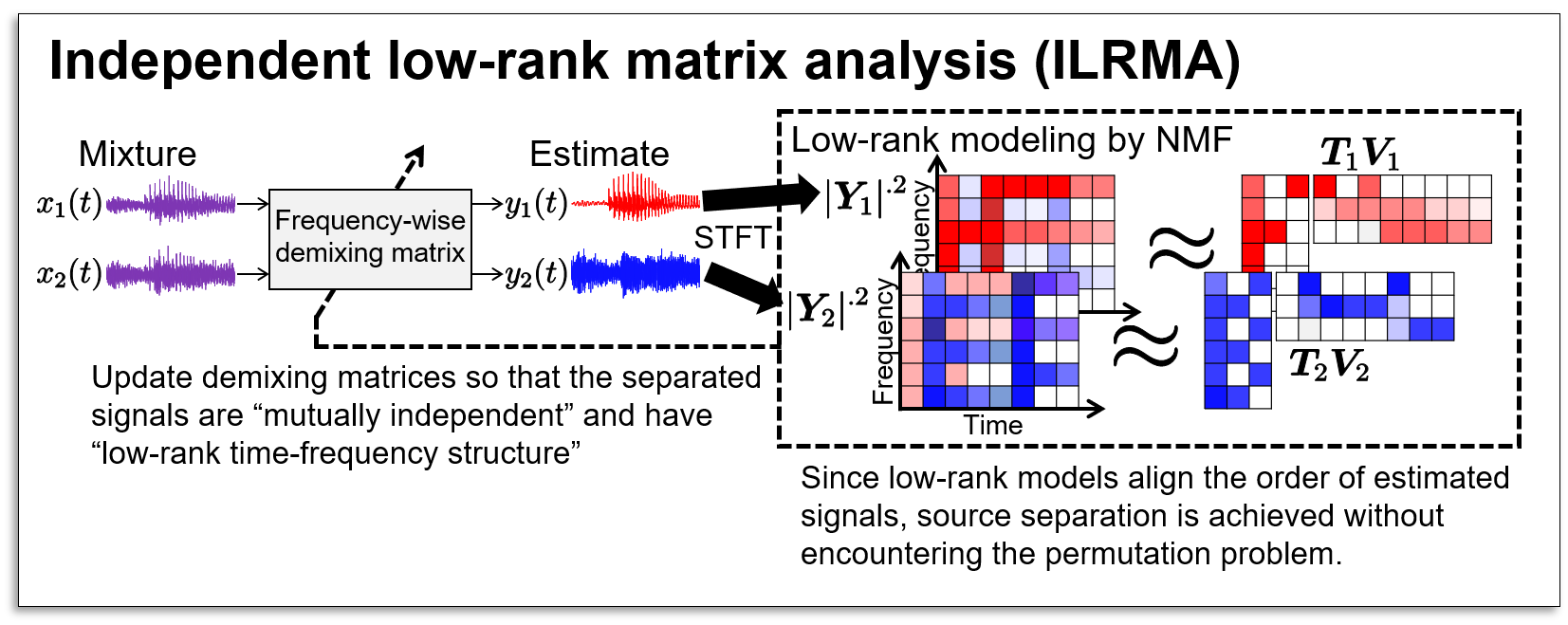
In the following demonstration, music sources are mixed using room impulse responses simulating the recording environment, and the separated results of IVA and ILRMA are presented. Also, we compare the performance of a state-of-the-art algorithm for BASS called multichannel NMF (NMF).
All the mixture signals are produced by convoluting E2A impulse response (rev. time: 300 ms) included in the RWCP database. We also show examples of computational times for each method, where the calculation was performed by Intel Core i7-4790 (3.6GHz) with MATLAB 8.3 (64-bit) and an iteration number of IVA, MNMF, and ILRMA was set to 200. In practical use, 30 and 100 iterations are sufficient for IVA and ILRMA, respectively. For MNMF, 200 iterations are still insufficient.
All the music signals in this demonstration were obtained from SiSEC and used only for an academic research purpose.
Two-source separation recorded by two-microphone array
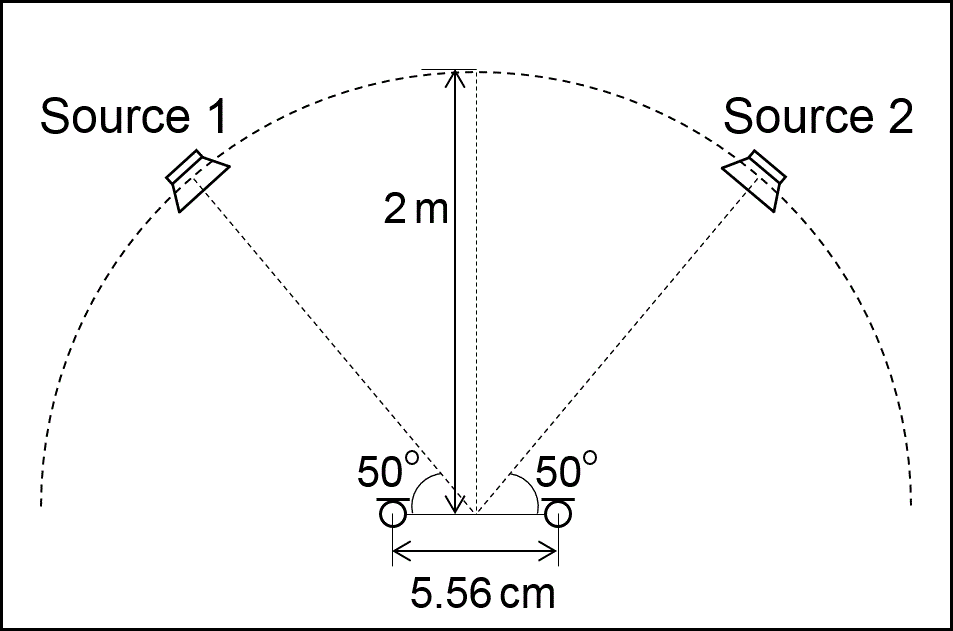
Input signal "bearlin/roads"
Separation by IVA (calc.: 42.2 s)
Estimated signal 2 (Vocals)
Separation by MNMF (calc.: 312.4 s)
Estimated signal 2 (Vocals)
Separation by ILRMA (calc.: 56.3 s)
Estimated signal 2 (Vocals)
Input signal "tamy/que pena tanto faz"
Separation by IVA (calc.: 39.8 s)
Estimated signal 2 (Vocals)
Separation by MNMF (calc.: 296.2 s)
Estimated signal 2 (Vocals)
Separation by ILRMA (calc.: 54.7 s)
Estimated signal 2 (Vocals)
Input signal "another dreamer/the ones we love"
Separation by IVA (calc.: 50.3 s)
Estimated signal 2 (Vocals)
Separation by MNMF (calc.: 459.8 s)
Estimated signal 2 (Vocals)
Separation by ILRMA (calc.: 76.5 s)
Estimated signal 2 (Vocals)
Input signal "fort minor/remember the name"
Separation by IVA (calc.: 46.3 s)
Estimated signal 2 (Vocals)
Separation by MNMF (calc.: 411.4 s)
Estimated signal 2 (Vocals)
Separation by ILRMA (calc.: 67.3 s)
Estimated signal 2 (Vocals)
Input signal "ultimate nz tour"
Separation by IVA (calc.: 51.7 s)
Estimated signal 2 (Synth)
Separation by MNMF (calc.: 478.8 s)
Estimated signal 2 (Synth)
Separation by ILRMA (calc.: 78.5 s)
Estimated signal 2 (Synth)
Three-source separation recorded by three-microphone array
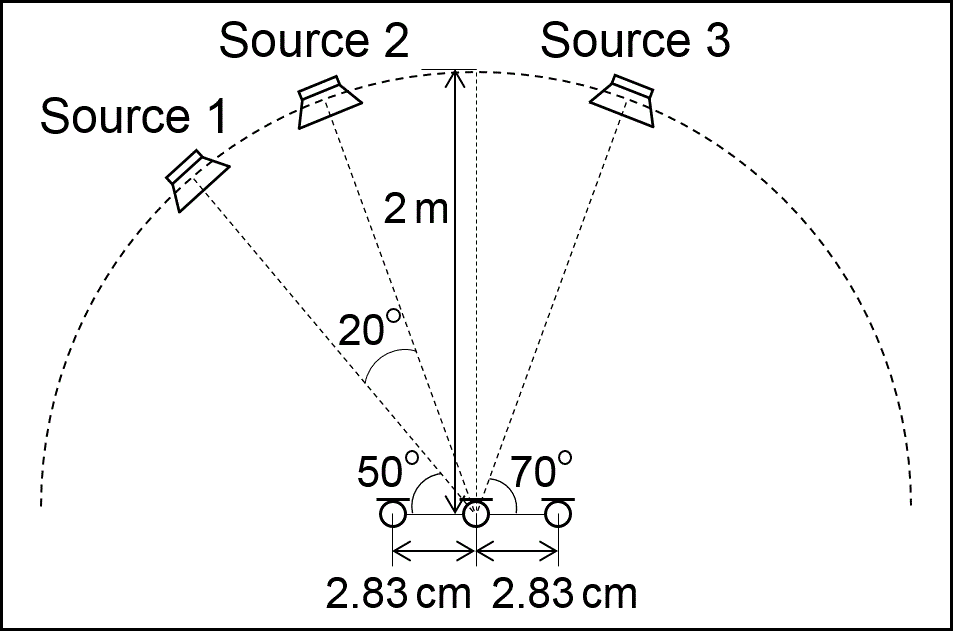
Input signal "bearlin/roads"
Separation by IVA (calc.: 91.6 s)
Estimated signal 2 (Bass)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 4498.4 s)
Estimated signal 2 (Bass)
Estimated signal 3 (Vocals)
Separation by ILRMA (calc.: 121.0 s)
Estimated signal 2 (Bass)
Estimated signal 3 (Vocals)
Input signal "another dreamer/the ones we love"
Separation by IVA (calc.: 106.0 s)
Estimated signal 2 (Guitar)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 8181.2 s)
Estimated signal 2 (Guitar)
Estimated signal 3 (Vocals)
Separation by ILRMA (calc.: 148.3 s)
Estimated signal 2 (Guitar)
Estimated signal 3 (Vocals)
Input signal "another dreamer/the ones we love"
Separation by IVA (calc.: 104.3 s)
Estimated signal 2 (Violin_synth)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 7909.7 s)
Estimated signal 2 (Violin_synth?)
Estimated signal 3 (Vocals?)
Separation by ILRMA (calc.: 147.6 s)
Estimated signal 2 (Violin_synth)
Estimated signal 3 (Vocals)
Input signal "ultimate nz tour"
Separation by IVA (calc.: 92.5 s)
Estimated signal 2 (Synth)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 5927.3 s)
Estimated signal 2 (Synth)
Estimated signal 3 (Vocals)
Separation by ILRMA (calc.: 127.1 s)
Estimated signal 2 (Synth)
Estimated signal 3 (Vocals)
Four-source separation recorded by four-microphone array
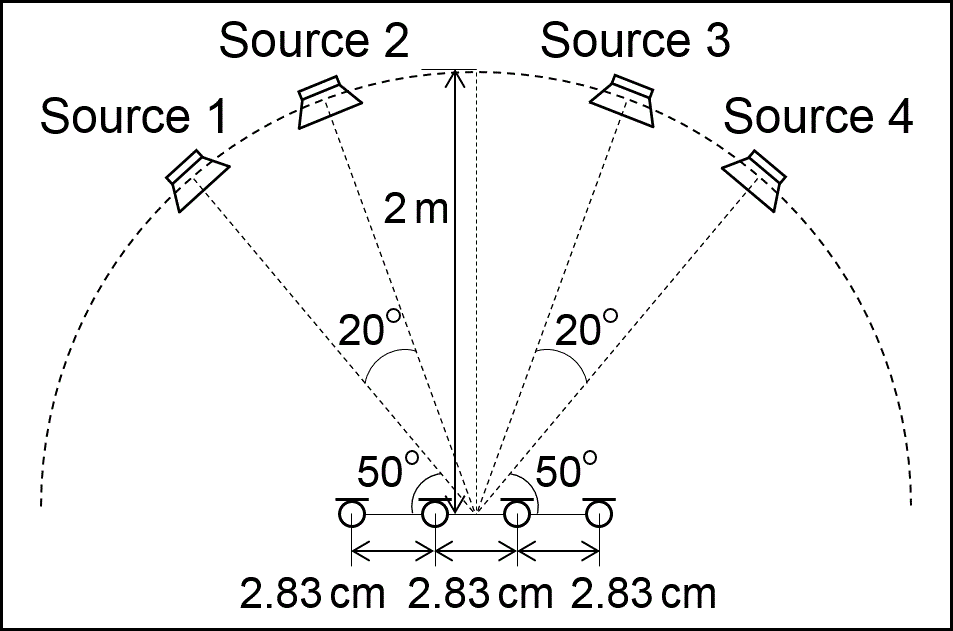
Input signal "fort minor/remember the name"
Separation by IVA (calc.: 147.6 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Violin_synth)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 10051.1 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Violin_synth)
Estimated signal 3 (Vocals)
Separation by ILRMA (calc.: 203.8 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Violin_synth)
Estimated signal 3 (Vocals)
Input signal "ultimate nz tour"
Separation by IVA (calc.: 131.6 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Guitar)
Estimated signal 3 (Vocals)
Separation by MNMF (calc.: 7618.6 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Guitar?)
Estimated signal 3 (Vocals)
Separation by ILRMA (calc.: 174.1 s)
Estimated signal 1 (Drums)
Estimated signal 2 (Guitar)
Estimated signal 3 (Vocals)
Source code
References
- ICA
-
- P. Comon, "Independent component analysis, a new concept?" Signal Process., vol. 36, no. 3, pp. 287–314, 1994.
- FDICA
-
- P. Smaragdis, "Blind separation of convolved mixtures in the frequency domain," Neurocomputing, vol. 22, pp. 21–34, 1998.
- IVA
-
- T. Kim, T. Eltoft, and T.-W. Lee, "Independent vector analysis: An extension of ICA to multivariate components," in Proc. Int. Conf. Independent Compon. Anal. Blind Source Separation, pp. 165–172, 2006.
- A. Hiroe, "Solution of permutation problem in frequency domain ICA using multivariate probability density functions," in Proc. Int. Conf. Independent Compon. Anal. Blind Source Separation, pp. 601–608, 2006.
- T. Kim, H. T. Attias, S.-Y. Lee, and T.-W. Lee, "Blind source separation exploiting higher-order frequency dependencies," IEEE Trans. Audio, Speech, Lang. Process., vol. 15, no. 1, pp. 70–79, 2007.
- IP in ICA or IVA
-
- N. Ono and S. Miyabe, "Auxiliary-function-based independent component analysis for super-Gaussian sources," in Proc. Int. Conf. Latent Variable Anal. and Signal Separation, pp. 165–172, 2010.
- N. Ono, "Stable and fast update rules for independent vector analysis based on auxiliary function technique," in Proc. IEEE Workshop on App. of Signal Process. to Audio and Acoust., pp. 189–192, 2011.
- MNMF
-
- H. Sawada,H.Kameoka, S.Araki, and N. Ueda, "Multichannel extensions of non-negative matrix factorization with complex-valued data," IEEE Trans. Audio, Speech, Lang. Process., vol. 21, no. 5, pp. 971–982, 2013.
- ILRMA
-
- D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Efficient multichannel nonnegative matrix factorization exploiting rank-1 spatial model," in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process., pp. 276–280, 2015.
- D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Determined blind source separation unifying independent vector analysis and nonnegative matrix factorization," IEEE/ACM Trans. Audio, Speech, and Lang. Process., vol. 24, no. 9, pp. 1626–1641, 2016.
- D. Kitamura, N. Ono, H. Sawada, H. Kameoka, and H. Saruwatari, "Determined blind source separation with independent low-rank matrix analysis," Audio Source Separation, S. Makino, Ed. (Springer, Cham, 2018), pp. 125–155.